Matrix Multiplication¶

Column Vector Factor Interpretation¶

Consider a $2 \times 2$ matrix M

$M = \left[ \begin{array}{cc} a & b \\ c & d \end{array} \right]$¶

Let's now consider the 2D Euclidean vector $(x, y)$. We can actually write this as a 2x1 "column matrix"

$ x = \left[ \begin{array}{c} x \\ y \end{array} \right] $¶

Now the dimensions line up so that we can do multiplication

$\left[ \begin{array}{cc} a & b \\ c & d \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} ax + by \\ cx + dy \end{array} \right] $¶

In this way, we see that a 2x2 matrix can really be thought of as a function from 2D vectors to 2D vectors. In fact, it's what's known as a "linear function."

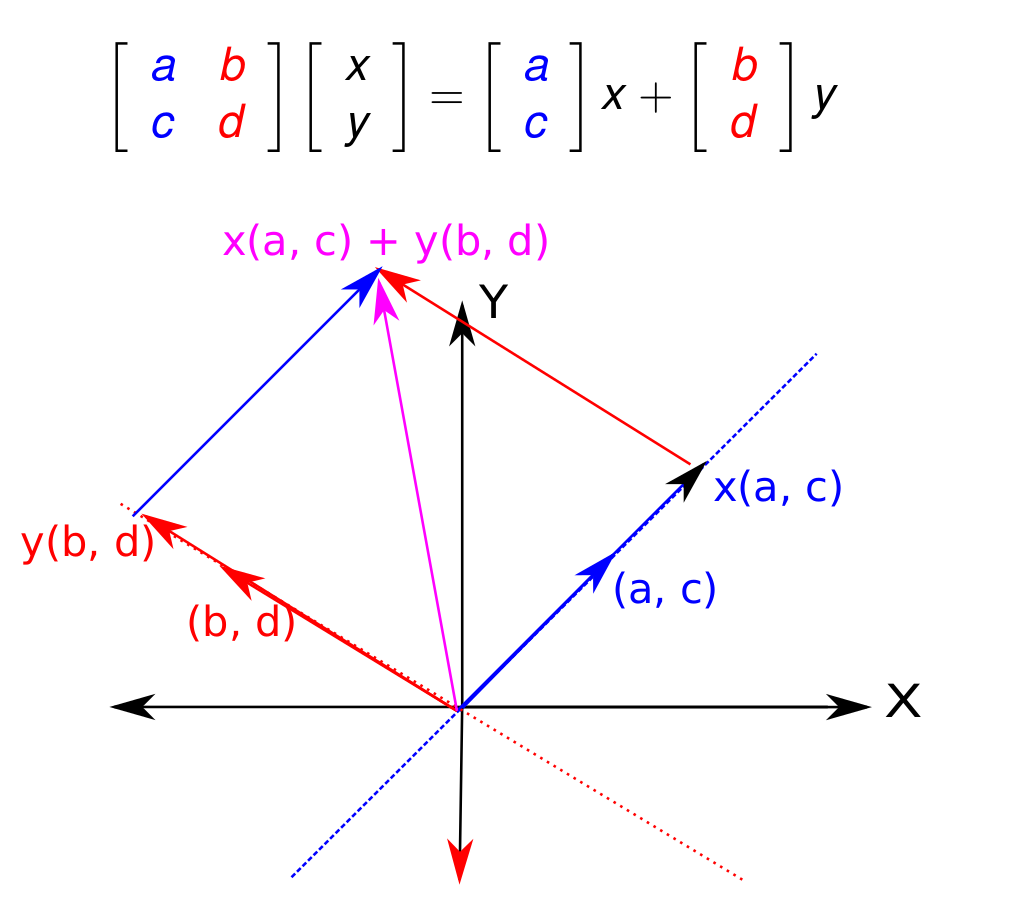
If we factor the above equation, we get a very interesting geometric interpretation of what this function is doing. In particular, we're just taking a scalar multiple x times the first column $(a, c)$, though of as a vector, plus a scalar mutiple y times the second column $(b, d)$. In other words, we walk along the first column vector of our matrix by a length of x, and then from where we end up, we walk s length of y along the second column. The picture below shows this.

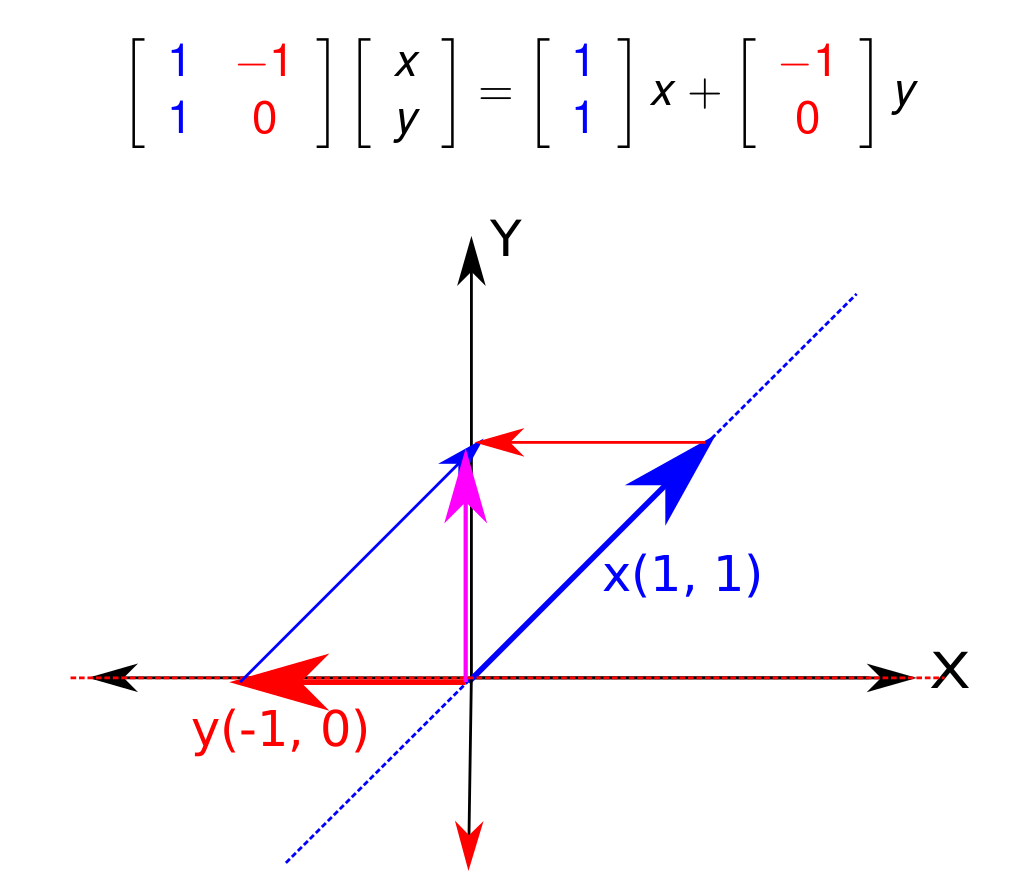
Below is a concrete example of the matrix multiplication

$\left[ \begin{array}{cc} 1 & -1 \\ 1 & 0 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} x-y \\ y \end{array} \right] $¶

In particular, if we multiplied the vector $(1, 1)$ on the left by this matrix, we would end up with the vector $(0, 1)$

This applies equally to any number of vectors in any dimensions. There are always as many rows as there are dimensions and as many columns as there are vectors we can use in our sum. For example, let's suppose we had 3 vectors in 4 dimensions. We could stack them up into a $4 \times 3$ matrix, and any vector we want to make that's a "linear combination" of these three vectors would be a multiplication on the right by a $3 \times 1$ matrix (we have a scalar for each column vector that says how much of it we want). Below shows such an example of 3 vectors in 4D with code to do it manually, as well as code to use matrix multiplication. You'll see they give the same answer

In [1]:

import numpy as np
v1 = np.array([1, 1, 0, 1])
v2 = np.array([1, 0, 0, 0])
v3 = np.array([0, -1, 0, 0])
x = 1
y = 2
z = -1
print(x*v1 + y*v2 + z*v3)

A = np.zeros((4, 3))
A[:, 0] = v1
A[:, 1] = v2
A[:, 2] = v3
print(A.dot([x, y, z]))

[3 2 0 1]
[3. 2. 0. 1.]