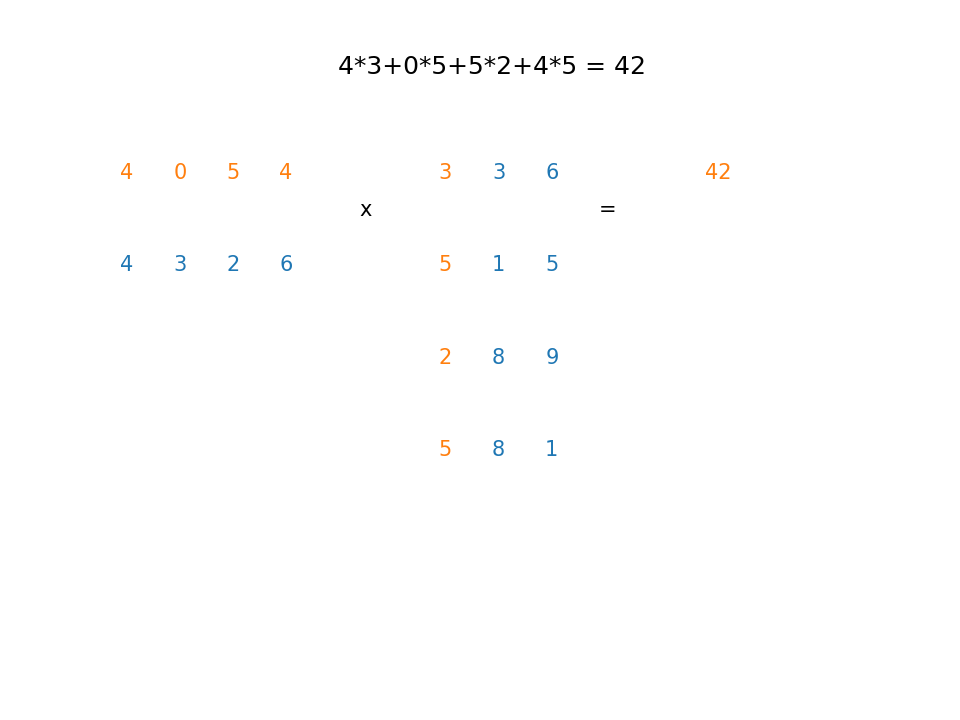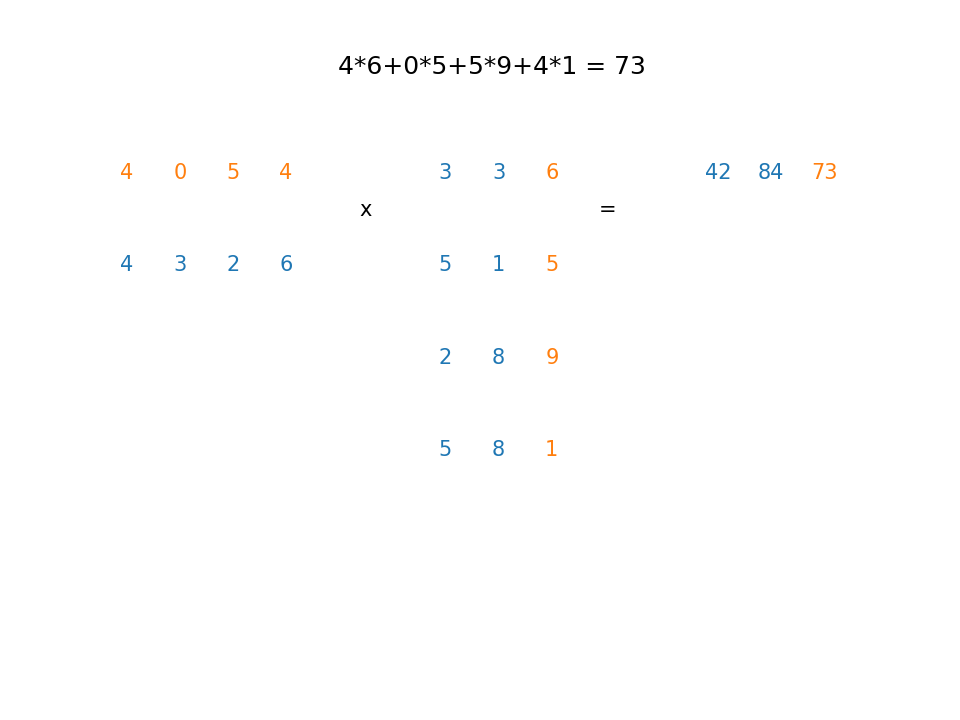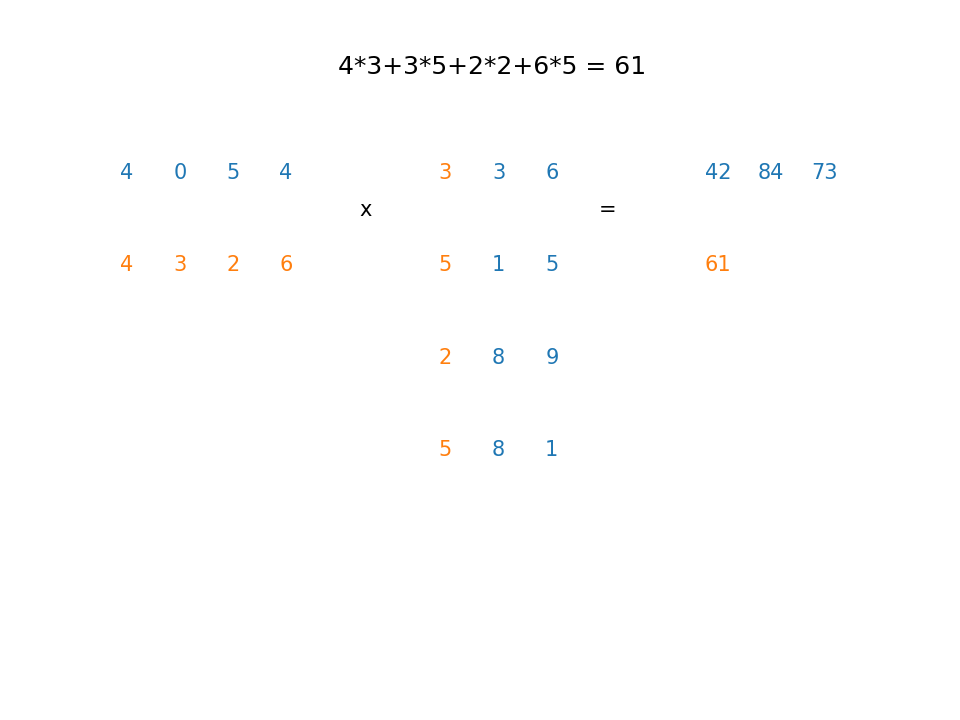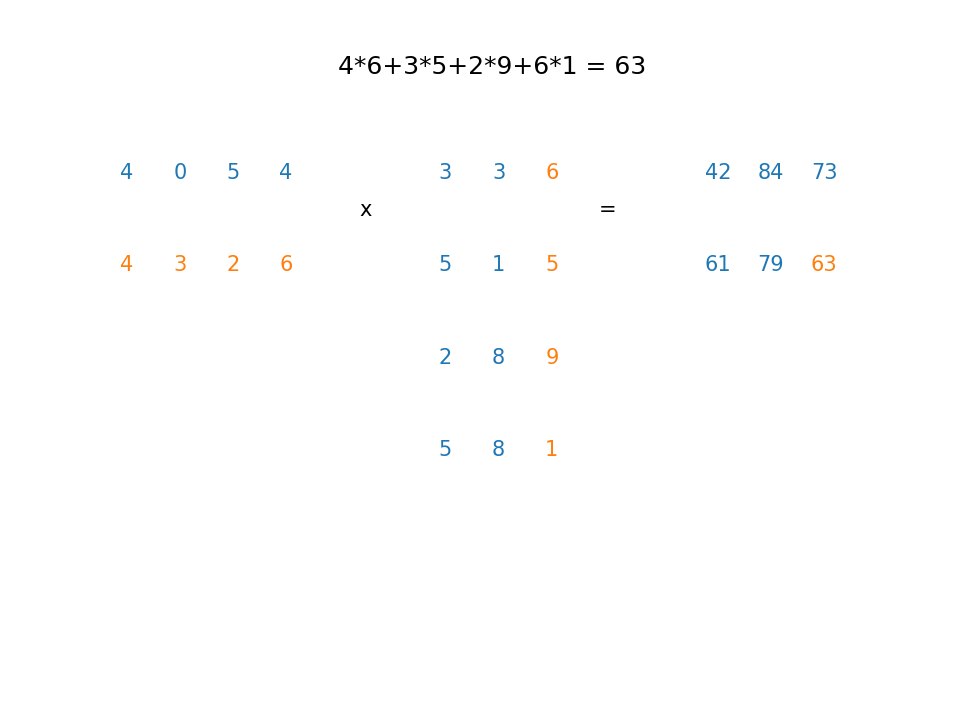Define matrix multiplication of an $M \times K$ matrix $A$ by a $K \times N$ matrix $B$ as the product $AB$, which is an $M \times N$ matrix, where
$AB[i, j] = A[i, :] \cdot B[:, j]$
The element $AB_{ij}$ is the dot product of the $i^{th}$ row of $A$ and the $j^{th}$ column of $B$
Below are a couple of examples
Example1¶
A $5 \times 3$ matrix multiplied by a $3 \times 4$ matrix yields a $5 \times 4$ matrix. For example, row 3, column 4 can be obtained as follows:
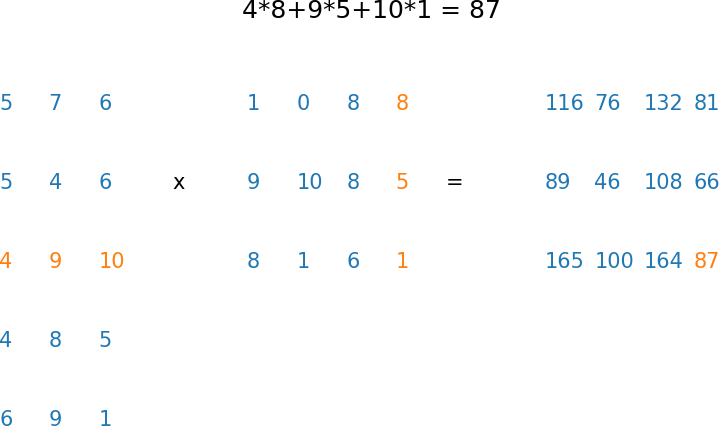
Here's an animation showing how to obtain the rest of the rows and columns (Click here to watch a youtube video where you can pause the frames if needed)
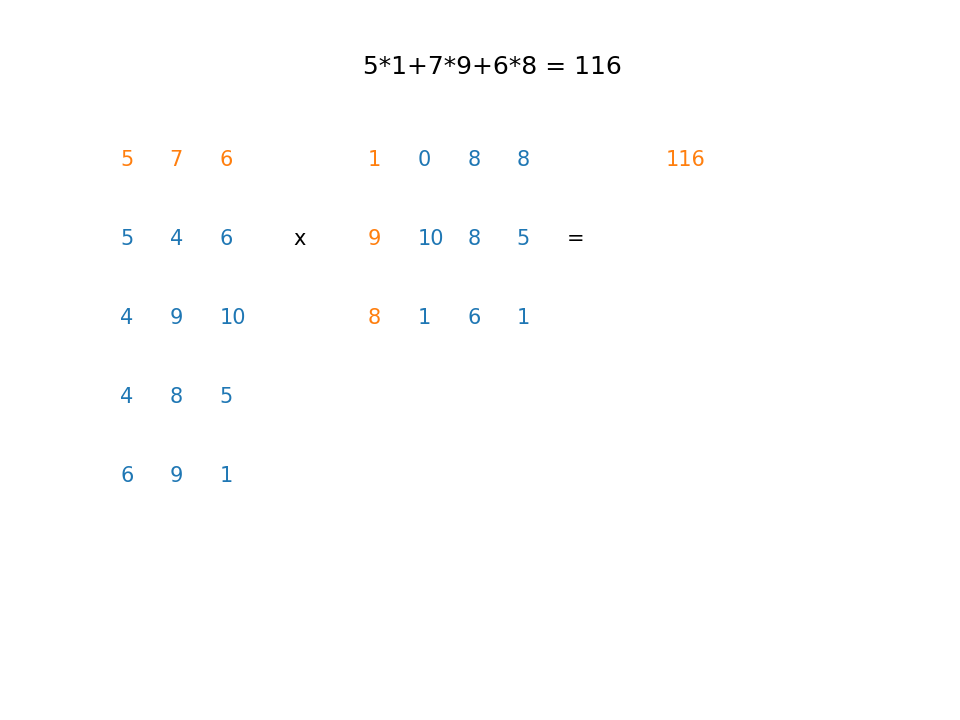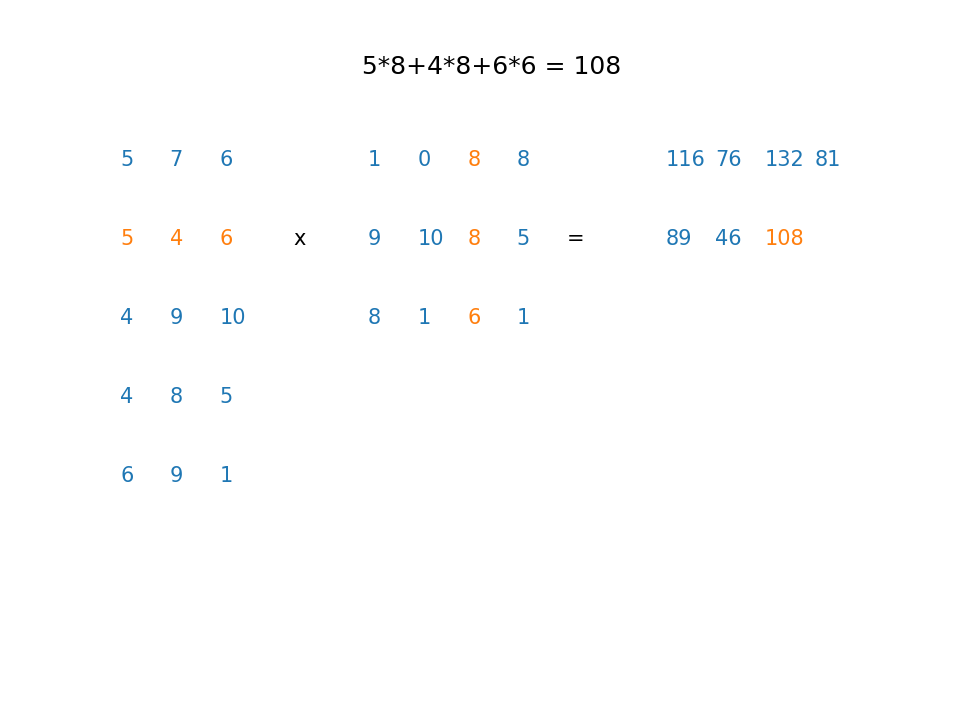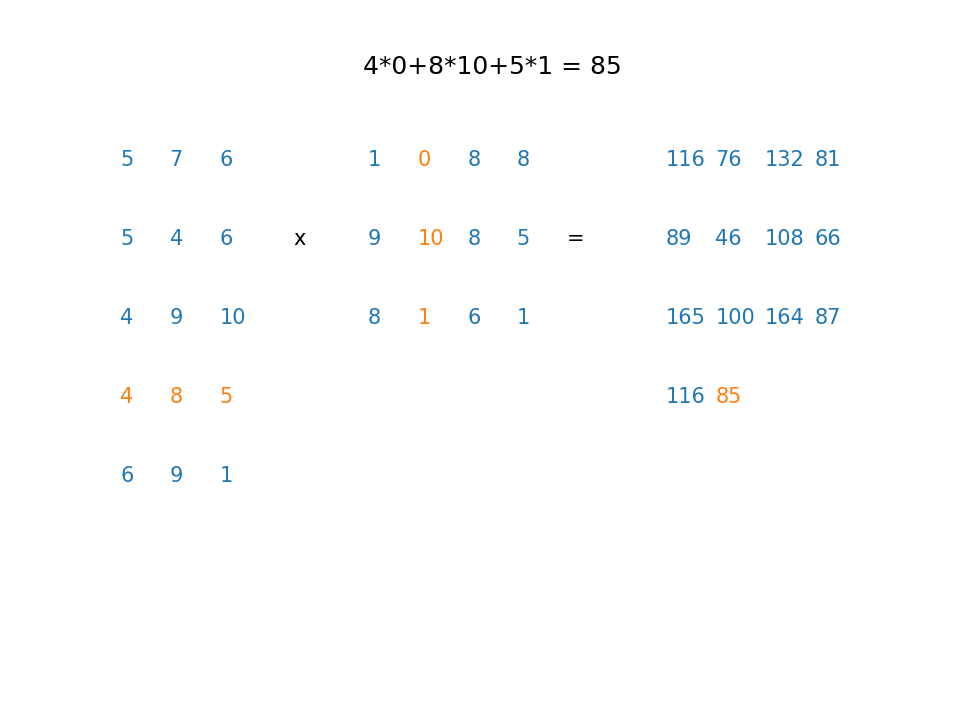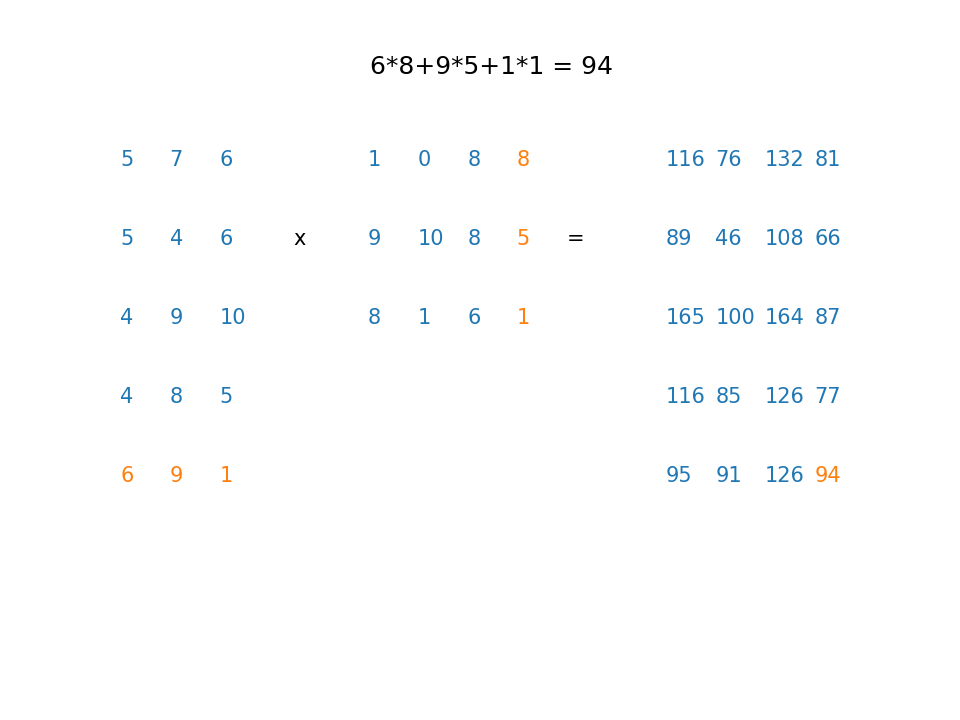
Example2¶
A $2 \times 4$ matrix multiplied by a $4 \times 3$ matrix yields a $2 \times 3$ matrix (Click here to watch a version of this video on youtube where you can pause the frames if needed)